Phương pháp giải
+ Nếu một đường thẳng vuông góc với một trong hai đường thẳng thì nó vuông góc với đường thẳng còn lại
+ Nếu hai đường thẳng cùng vuông góc với một đường thẳng thì hai đường thẳng đó song song với nhau.
+ Hai góc cùng phụ một góc thì hai góc đó bằng nhau.
Nếu hai góc có cạnh tương ứng song song thì:
+ Chúng bằng nhau nếu hai góc cùng nhọn hoặc cùng tù.
+ Chúng bù nhau nếu góc này nhọn và góc kia tù.
Giải chi tiết
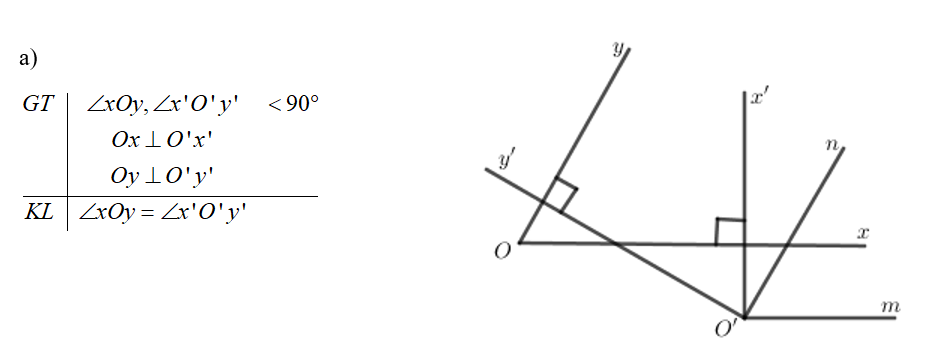
Chứng minh:
Vẽ \(O'm//Ox\) và \(O'n//Oy\)
Vì \(\left\{ \begin{array}{l}O'x' \bot Ox\\O'm//Ox\end{array} \right.\) nên \(O'x' \bot O'm\)
Suy ra \(\angle mO'x' = 90^\circ \left( 1 \right)\)
Vì \(\left\{ \begin{array}{l}O'y' \bot Oy\\O'n//Oy\end{array} \right.\) nên \(O'y' \bot O'n\)
Suy ra \(\angle nO'y' = 90^\circ \left( 2 \right)\)
Ta có: \(\left\{ \begin{array}{l}\angle mO'x' = \angle mOn + \angle nO'x' = 90^\circ \\\angle nO'y' = \angle x'O'y' + \angle nO'x' = 90^\circ \end{array} \right.\)
Suy ra \(\angle x'O'y' = \angle mOn\) (cùng phụ với góc \(\angle nO'x'\))
Vì \(\left\{ \begin{array}{l}O'n//Oy\\O'm//Ox\end{array} \right.\) nên theo kết quả của bài 9, ta có: \(\angle xOy = \angle mOn\). Mà \(\angle x'O'y' = \angle mOn\)
Suy ra \(\angle xOy = \angle x'O'y'\left( { = \angle mOn} \right)\) (đpcm)
Chứng minh:
Vẽ \(O'm//Ox\) và \(O'n//Oy\)
Vì \(\left\{ \begin{array}{l}O'x' \bot Ox\\O'm//Ox\end{array} \right.\) nên \(O'x' \bot O'm\)
Suy ra \(\angle mO'x' = 90^\circ \left( 1 \right)\)
Vì \(\left\{ \begin{array}{l}O'y' \bot Oy\\O'n//Oy\end{array} \right.\) nên \(O'y' \bot O'n\)
Suy ra \(\angle nO'y' = 90^\circ \left( 2 \right)\)
Ta có: \(\left\{ \begin{array}{l}\angle mO'x' = \angle mOn + \angle nO'x' = 90^\circ \\\angle nO'y' = \angle x'O'y' + \angle nO'x' = 90^\circ \end{array} \right.\)
Suy ra \(\angle x'O'y' = \angle mOn\) (cùng phụ với góc \(\angle nO'x'\))
Vì \(\left\{ \begin{array}{l}O'n//Oy\\O'm//Ox\end{array} \right.\) nên theo kết quả của bài 9, ta có: \(\angle xOy + \angle mOn = 180^\circ \). Mà \(\angle x'O'y' = \angle mOn\)
Suy ra \(\angle xOy + \angle x'O'y' = 180^\circ \) (đpcm)
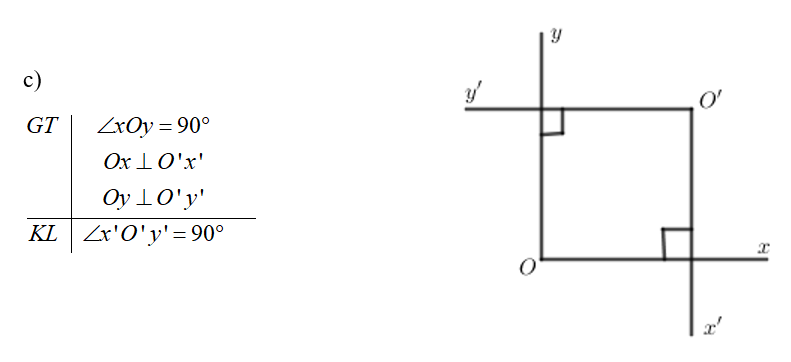
Chứng minh:
Vì \(\left. \begin{array}{l}Oy \bot Ox\\O'x' \bot Ox\end{array} \right\} \Rightarrow Oy//O'x'\)
Vì \(\left. \begin{array}{l}Oy//O'x'\\Oy \bot O'y'\end{array} \right\} \Rightarrow O'x' \bot O'y'\)
\( \Rightarrow \angle x'O'y' = 90^\circ \) (đpcm)
